We work in collaboration with the Procter & Gamble Company to understand the flow and breakup of complex fluids. In particular, we study the pinch-off dynamics of fluids (e.g. lyotropic surfactants and thermotropic liquid crystals) possessing liquid crystalline order.
When mixed with water, surfactants can form a variety of phases, including ones with lamellar (smectic-A) liquid crystalline order. We have performed experiments studying the process by which these materials breakup into droplets. These fluids are particularly relevant, not only because of the interesting physics, but because fluids with microstructure such as these are commonly used in industrial processes.

When water drips from a faucet, a singularity is formed at the point of pinch-off [see movie of water dripping below]. In the region of the singularity, the minimum radius decreases with time to pinch-off as a power-law. The axial scale exhibits the same power-law behavior and the drop profile is conical. The independence of a length scale suggests that successive drop profiles should collapse onto eachother, which is indeed the case [see droplet papers and references within on our publications page]. Similar experiments performed on other Newtonian fluids with varying viscosity have shown similar behavior. A common thread of these fluids is that they are all isotropic with constant viscosity.
By using anisotropic fluids with liquid crystalline order to study drop pinch-off, we can expand the current understanding of drop pinch-off macro-dynamics by introducing fluid microstructure. We use the liquid bridge geometry to study the pinch-off [see plots and movie below]. Amazingly, we find a new universal scaling behavior in the lamellar phase in which both the minimum radius and axial scale decrease with time to pinch-off as power-laws. We find universal scaling behavior in which successive bridge profiles scale onto a single similarity solution. We also find that, unlike Newtonian fluids pinching in air, no satellite droplet is formed during pinch-off.
The cartoon and images below show the liquid bridge geometry (a) and images of the lamellar phase during (b,c) and just after pinch-off (d). The relevant scaling parameters are the minimum radius Rmin, the axial lenth scale z, and the bridge profile h(z,t).
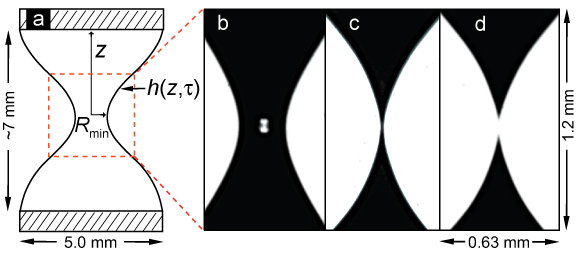
As seen in (a) below, the minimum radius Rmin decreases with time to pinch-off as a power-law with exponent of 0.62. We then conduct a scaling analysis and look for universal scaling behavior. First, we define H = h(z,t)/Rmin. This definition ensures that for each time the profile vertex is at (x,y)=(1,0), as seen in (b). The four curves are for the times indicated by arrows in (a). We then determine the axial scaling by first defining z*=z-z0 (where z0 is the location of Rmin) and then extracting the z* values at H=2 (c). We find that z* versus time to pinch-off also scales as a power law with exponent of 0.36. Using the axial scaling, we scale the vertical axis by t0.36 or equivalenty Rmin0.58 in (d). (d) shows that indeed this scaling collapses the bridge profiles onto a single similarity solution.

We have performed continous bulk rheological expermiments and find the stress varies with shear rate with the same power-law as the minimum radius with time to pinch-off in our liquid bridge experiments (see below). These results agree with recent theories [see the references within our paper on the publications page]. We now have the first experimental evidence that such fluids shear thin with the same rate dependent viscosity in both bulk and extensional flows.
By introducing a new imaging configuration, we can utilize the birefringent nature of these materials and image the alignment of the lamellar grains during the pinch-off process. Shear thinning in lamellar fluids can occur when the grains align along the shear direction. The pictures below are before (a) extension and during (b) final pinch-off. Our new imaging configuration confirms that indeed the lamellar grains are aligning along the axial flow direction.

We have shown that the universal behavior is in fact partial: we can break it down. The universal behavior will break down at the size of the lamellar domain, which we can change by pre-shearing the fluid. The images below show the birefringence before breakup (a) and an image of the bridge profile just prior to pinch-off (b). The large yellow streak in (a) shows how before pinch-off, the lamellar grains have already coarsened. The difference in bridge profile in (b) occurs when the minimum radius is approx. 10 microns. At this point, the region of the minimum radius elongates and the rate of thinning decreases.

To generalize these results, we have performed equivalent experiments with the thermotropic liquid crystal 8CB. At room temperature 8CB is in the smectic-A phase, having the same mathematical order as the lamellar phase. The image below shows the fluid just prior to pinch-off. As with the lamellar phase, 8CB in the smectic phase shows universal scaling behavior in which bridge profiles collapse onto a single similarity solution. Bulk rheology experiments have shown that the stress varies with shear rate with the same power-law as we find for the minimum radius versus time to pinch-off. Also equivalent with the lamellar phase, this universal behavior breaks down when the fluid is pre-sheared.

As a final test of the role played by the smectic-A liquid crystalline order in the pinch-off dynamics, we have also performed experiments on 8CB in the nematic phase. For the nematic phase, the pinch-off dynamics are completely different. During final pinch-off, the minimum radius versus time to pinch-off initially scales as a power-law with slope approx. 1.50, and then the thinning of the bridge slows significantly. Unlike the lamellar phase of surfactant and the smectic-A phase of 8CB, there is a satellite drop produced in the nematic phase of 8CB ( images below). The pinch-off behavior in the nematic phase of 8CB is equivalent to the behavior seen in the dense micellar (just below the isotropic-hexagonal transition) and the reverse-micellar phases of the surfactant system. The similarities in the nematic phase of 8CB and the dense micellar/reverse-micellar phases of the surfactant system suggest that the micelles/reverse-micelles act like rigid rods and not 'wormlike' micelles. We are currently working on a concise explanation for this.

