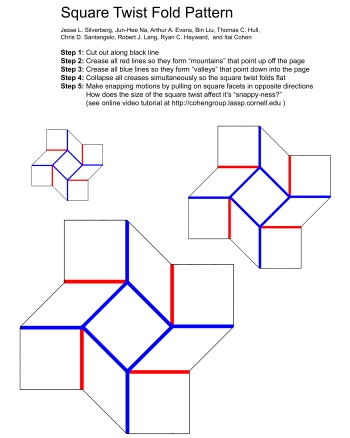
Drawing on the art of origami to inspire mechanical metamaterials relies on the ability to extract useful design principles from crease patterns. One particularly interesting pattern is the square twist. Not ony is it tessellatable, but the unit highlighted below has some surprsing properties.
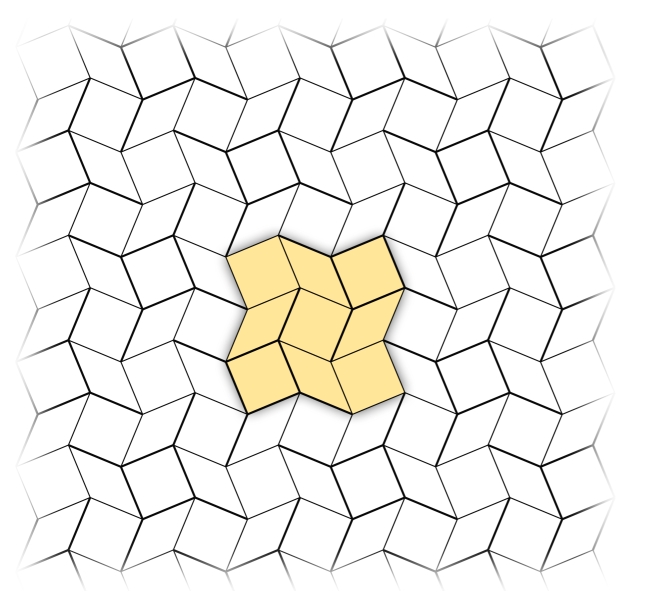
The square twist tessellation and a highlighted unit. Note the mountain-valley crease assignment shown here by thick and thin lines is just one possible tessellation. Other mountain-valley crease assignments, such as the one used this work and shown below, are also tessellatable.
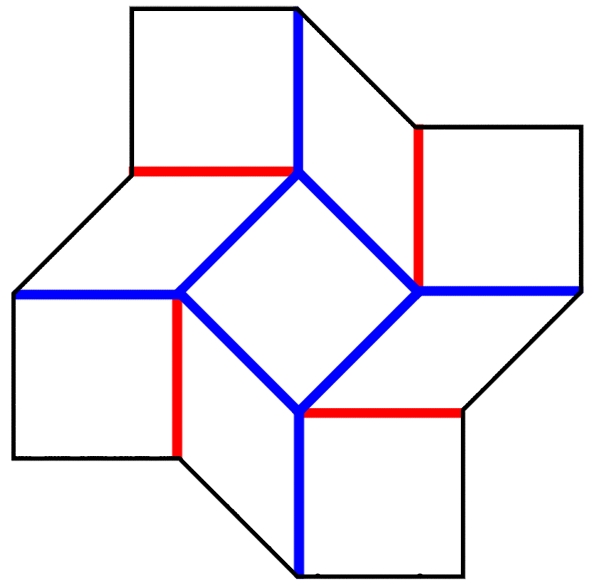
A single unit from the square twist with mountain and valley folds shown as red and blue lines. Scroll down for a print-and-fold version that can made at home.
Mathematically speaking, the square twist folding pattern is unfoldable. Meaning, the crease geometry has a built-in incompatibility that rigidly locks the creases in place. However, as shown in the photographs below, the square twist can definitely be folded.
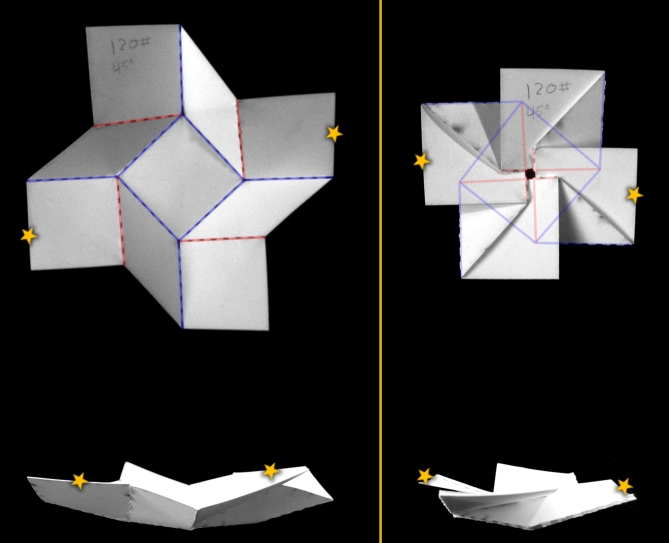
These top- and side-view images of a square twist in the unfolded (left) and folded (right) configurations show the crease pattern can be folded contrary to predictions based on the crease pattern alone. Gold stars highlight points that can be compared across images.
If the math tells us the square twist can not be folded, but the experiments tell us otherwise, how do we understand the differences? The movies below illustrate the transitions between folded and unfolded configurations while giving big hints at what's happening.
This video shows a square twist with strong bistability between the folded and unfolded states.
This video shows a square twist with weak bistability between the folded and unfolded states.
Evidently, there's a snapping transition between folded and unfolded states. The difference between these two movies has to do with the angles of the crease pattern and suggests the bistable nature of the square twist is a geometry-dependent phenomenon. To quantitatively understand the snapping transition, we set up a series of experiments measuring the force-extension relation as a function of geometry and material properties. This movie below illustrates the basic experiment.
This video shows an experiment where we simultaneously unfold a square twist while measuring its force-extension relation. This data allows us to measure the mechanical properties of origami structures as a function of the crease pattern's geometric properties.
From these experiments, we found the bistability between folded and unfolded states can be tuned by the crease pattern's geometry, and that a geometric phase transition between monostability and bistability is possible. The underlying mechanism enabling the structures to be folded is a set of additional degrees of freedom hidden from the crease pattern that arises from the fact that flat portions of paper between creases can be bent. By tuning the geometry, the amount of bending is adjusted, and hence the strength of the bistability can be enhanced or minimized. Because bending is not described by the crease pattern alone, the bending-mechanism remained hidden from the mathematical analysis that predicted the square twist to be rigid and unfoldable. This experimental understanding can be tested in simulations that probe the geometry- and material-dependence of the square twist's snapping action.
Experimental measurements indicate mechanical bistability in the square twist is driven by an energetic cost of bending paper during the unfolding process. This video shows a simulation where we test this idea by measuring the total energy as the square twist is unfolded.
These simulations are consistient with our experimental understanding and produce force-extension curves that are qualitatively and quantitatively similar. Indeed, they even predict a ratio of bending and creasing energy scales that is verified in our experiments. Moreover, the geometrically-driven bending interpretation also predicts that square twists should exhibit hysteresis in open-fold cycles under the right conditions. In collaboration with the Hayward lab at UMass Amherst's Department of Polymer Science and Engineering, we looked for and found the predicted hysteresis in a sub-mm self-folding polymer gel version of the square twist. Thus, this combined experimental and theoretical work extracts a generic design principle that could potentially be useful for mechanical metamaterial applications.
Now that you've read about the project, try making your own square twist and experiment with bistability at home! Click the thumbnail below for a printable PDF.
Read the article published in Nature Materials here.
Read the Nature Materials News & Views piece here.
Read the article in the Cornell Chronicle here.